2021年の振り返り
今年は、20歳のときに立てた目標を達成した年だった。
目標だった年商1000万円は、本業と副業の両立によって達成できた。 数年前は単価1,500円程度で請けていたが、レベルアップと交渉を遂げて単価5,000円~6,000円に上げたことが大きかったように思える。
日常的には、本業の時間以外はだいたい副業に充てていたため、非常に忙しかった。とくに解決が困難な課題に副業でぶち当たったりしたとき、誰にも相談できない苦痛は耐え難かった。ひたすらに文献を読み漁り、人に聞き、解決法を探した。
小手先のテクニックに頼り、基礎の理解が不十分だと気づいた。来年はそれを改善したい。
1,000万円という額面はもちろん嬉しいが、ちゃんとそれだけの価値提供をできたことが一番嬉しい。
正直、今年は副業にかまけていたが、会社でも立ち振る舞いが評価されて昇級し、給与が驚くくらい上がった。 ベンチャー企業に勤めていたので、金額は期待していなかったがいい意味で期待を裏切られた。とても嬉しかった。
健康面は、ふたたび腸閉塞をやらかしてしまい、10日間入院した。
来年は、健康に気をつけたい。
からあげさんの『ゼロから始める情報発信: No Output, No Value』という書籍を読了した
ブログが継続しないなぁと思っていたところ、AIへの取り組みでよく見かけていたからあげさんが情報発信についての書籍を書いていた。
ブログ継続に関する書籍は多いが、僕と同じソフトウェアエンジニアが書いている書籍を読んだことがなかったので興味が湧いた。
書いてある内容に目新しさはなかったけれど、ところどころに引用された偉人たちの金言が胸に刺さった。
そこから取り上げるのは 徒然草 第百五十段 。ここに書かれていることは学生時代によく目にしたが、いまになると余計耳が痛く感じた。
2020/06/29 今日の学び
転職してから29日目。最初こそ苦労したが、いまは前職の延長のことをしている。やっていることはあまり変わらない。マンネリ化しないようにたくさん挑戦したい。
今日は、神田昌典のマーケティングの本を少し読んだ。マーケティングの名著だというが本当か。タイトルに「90日で儲かる」などと入っており、少々不安。
エモーショナルマーケティングとは、あなたがお客を探す方法ではない。お客があなたを探す方法だ、と前に説明した。
納得。だが、いまどきそれが当たり前のような気がしている。

この図は、「お客は、最初からあなたにお金を払おうとは思っていない。適切な段階を用意し、最終的にお金を払ってもらうよう設計する」ことを示している。この設計が大事だと、本では主張している。
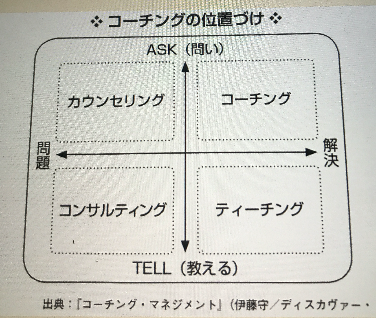
コーチングについて
スタート地点
コーチングは、相手の考えを引き出して行動へつなげることだとざっくり知っていた。 私の先入観では、「人に伝えるためにしゃべることで思考が整理され、自己解決する」ラバーダッキングと似たようなものだと思っていた。 その気になれば、ルールに従った機械的な応答を返すだけでもある程度目標が達成できるのではないか?と考えていた。 「来談者中心療法のセラピスト」のように振る舞えるELIZAのように。
現状の理解
コーチングはcoacheeの中の知識を引き出し、行動を促し問題解決するためのものである。知識を与えたり問題を見つけるものではない。目標がなければ向かない。 コーチングは定期的に行う。coacheeの目的が整理され、目標が決まり、定期的にどうなっているか話をする。
読んだ本
学び
コーチの投げかける質問にクライアントの視点が変わり、物事がはっきりし、発想が膨らみ、そして行動を起こす意欲が湧いてくる。そのようなプロセスを作り出すことがコーチに求められる支援のあり方と言えるでしょう。
コーチングは教わらない。問題を見つけない。問い、解決に導く。
> コーチングは「知識と行動の間に横たわる溝」に橋をかける試みと言えるでしょう
コーチングは行動を促し、目標達成に導く。coacheeに知識を与えることが主目的ではない。 コーチングが有効に働く例として、知識が増えスキルも上がり意欲が弱まっている人が挙げられていた。
「あなたの話を聞いていて、あなたは◯◯◯という期待や目的をもっているように感じる。そこを目指してみるのはどうか」と提案することも役立つでしょう。
コーチングは、目標がない場合に有効に働かない。やりたいことがないならコーチングは向かない。対話を通じてcoacheeが持っている目的を提案することで意義のある時間になる。
簡単にまとめると、コーチングを通じてcoacheeの目的は整理され、coarchee自身が目標を設置する。coacherは定期的に話をしてモニタリングする。
ここまでがコーチングにおけるセットアップ。コーチングはセットアップ、実践、振り返りという3つのフェーズに分かれている。
モニタリングするときの観点が三つある。
クライアントの状態を把握するためコーチは3つの視点をもっています。それは、
・ポゼッション、身につけるもの ・ビヘイビア、行動 ・プレゼンス、考え方、信念
という視点です。これを「PBPの視点」と呼びます。
ポゼッション、ビヘイビア、プレゼンスの三つ。
ポゼッションの視点からコーチのする質問として、以下のようなものがあります。
・理想の状態に近づくために自分に必要なものは何ですか? ・目標達成のためにはどんな分野の情報が必要ですか? ・自分がいまもっている知識やスキルで使えそうなものは何ですか?
ポゼッションは、スキルや技術、知識の視点。目的と目標を達成するために何が必要かcoacheeに気づいてもらう。いわば、努力の方向のキャリブレーション。
コーチはクライアントがどんな行動をするか、どれくらい行動しているかなどのBehaviorに注目しコーチングを進め目標達成を支援します。たとえば、コーチのする質問として以下のようなものがあります。
・やろうと思っていて実行できないことは何ですか? ・目標を達成するために今日からできることは何ですか? ・次回のセッションまでにどんなことをやりますか?
ビヘイビアは、行動の視点。知識と行動のギャップをcoacheeに把握してもらう。目標達成に必要な取り組みの確認と同意。
Presenceについてコーチのする質問としては以下のようなものがあります。
・あなたが大事にしている価値観は何ですか? ・環境の変化に合わせて、自分が変化すべきことは何でしょうか? ・その目標を達成することは、あなたにとってどんな意味がありますか?
プレゼンスは、目標達成を邪魔する意識に気づかせること。「人の時間を無駄にしてはいけない」というプレゼンスのもとに「人に聞かずに一人でやる」という行動をしていたりする。目標達成はときにはマインドセットを変えないといけないことを表している。
今日はここまで。
2020/06/26 今日の学び
転職してから26日目。仕事が終わったあと、前職メンバーと飲み会をした。みんな元気そうでよかった。みんな仲良くしてくれてとてもいい。ずっとつながっていたい。
高校生の情報の教科書に、データサイエンスの内容が含まれている。僕はそこを押さえていないのでとても焦りを感じた。 www.mext.go.jp